从OOP切换到FP风格确实需要改变思维方式。在FP中,你不再有那些常用的原语,比如类、可变变量、循环等等。在最初的几个月里,你的效率不会很高,你会因为一些简单的事情卡上几个小时或几天,而这些事情以前通常只需要几分钟。这会很困难,你会觉得自己很愚蠢。我们都是这么过来的。但是度过这段时间后,你将获得超能力。我没听说过有谁是在每天做FP之后,又从FP转回OOP的。你可能会切换到一种不支持FP的语言,但你仍然会使用FP概念来编写代码,就是这么好。
在本文中,我将尝试分解一下概念,并回答在学习FP时困扰我的常见问题。
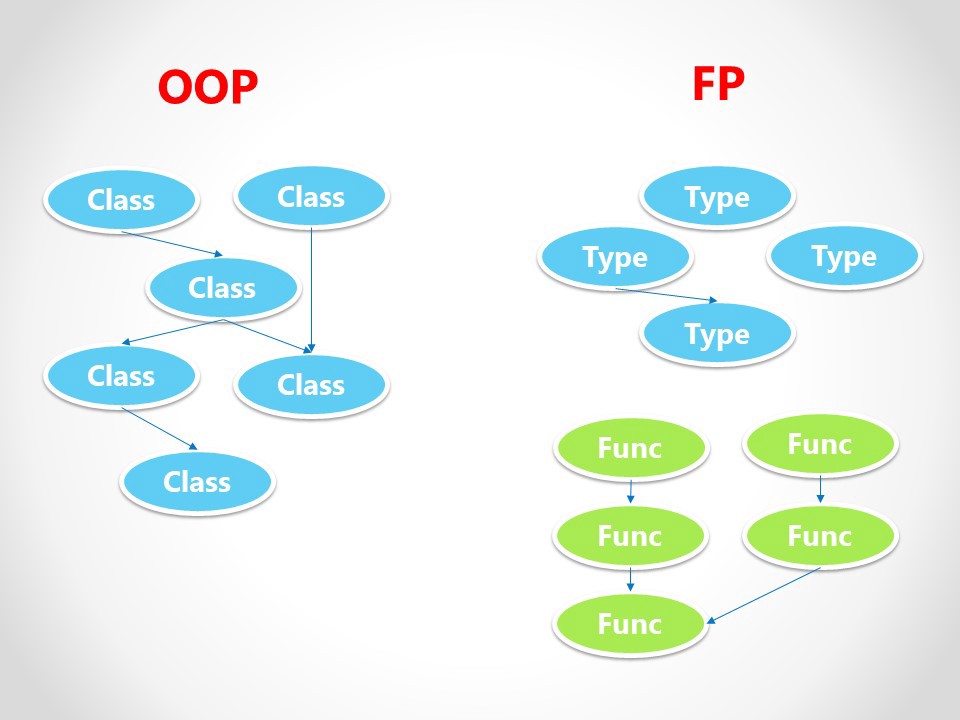
1、这里没有类
Q:没有类?那我怎么组织代码呢?
事实证明,你不需要类。就像在旧的良好的面向过程编程中,你的程序只是一个函数的集合,区别在于,在FP中这些函数必须包含一些属性(稍后讨论),它们也必须互相组合。你会经常听到 “组合 “这个词,因为这是FP的核心思想之一。
我建议你不要再考虑“创建类的实例”或“调用类的方法”。你的程序将只是一堆可以互相调用的函数。
题外话:很多FP语言都有一个“类型类”的概念,不要与OOP中对类的理解相混淆。类型类的目的是为了提供多态性。一开始你还不必担心该问题,但是如果你感兴趣,请参阅文章:Type classes explained。
Q:数据呢?我通常汇总一个类里面保存一些数据和修改这些数据的函数。
对此,我们有代数数据类型(Algebraic Data Types ,ADT),这只是对持有数据的记录的一个花哨名称。
case class Person(name: String, age: Int)data Person = Person String Int
-- OR
data Person = Person
{ name :: String
, age :: Int
, address :: Address
}你可以把它看作是一个只有构造函数的类。用FP术语来说,它们是“类型”,而构造函数称为“类型构造函数”。下面是构造类型并从中获取值的方法:
case class Person(name: String, age: Int)
// Using type constructor
val person = Person("Bob", 42)
// Accessing fields
val personsAge = person.agedata Person = Person
{ name :: String
, age :: Int
, address :: Address
}
-- Using type constructor
person = Person "Bob" 42
-- Or using records notation
person = Person {name = "Bob", age = 42}
-- Accessing fields
personsName = name person -- "Bob"注意,在Haskell中,name和age实际上是接受Person类型的值并返回其字段的函数。
Q:好吧,但我如何改变这个人的年龄呢,举例说明下?
在原地修改数据(在命令式编程理念中)是一种突变,而在FP中你不能执行突变(后面会有更多介绍)。如果你想改变什么东西——你可以复制一份。
val bob = Person("Bob", 42)
// .copy provided by the 'case class'
val olderBob = bob.copy(age = 43)bob = Person "Bob" 42
olderBob = bob { age = 43 }有2种类型的ADT值得了解:乘积型与和型。
乘积类型:一个字段的集合,要构造一个类型,必须指定所有字段。
// Person is a product type consisting of 3 fields case class Person(name: String, age: Int, address: Address) // Address on its own also is a product type case class Address(country: String, city: String, street: String) // In order to create a Point you have to provide all 3 arguments case class Point(x: Double, y: Double, z: Double)-- Person is a product type consisting of 3 fields data Person = Person { name :: String , age :: Int , address :: Address } -- Address is a product type on its own data Address = Address { country :: String , city :: String , street :: String } -- In order to create Position you have to provide all 3 coordinates data Position = Position { x :: Integer , y :: Integer , z :: Integer }和类型:表示可选性。你的类型可以是某一数据或者其它数据。例如,形状可以是圆形或方形。
// Scala doesn't have a nice syntax for sum types so // it looks like a familiar OOP inheritance tree. sealed trait Shape // But don't get confused: the 'extends' here stands for 'is' // relationship, not in a sense of 'extends and overrides methods'. // It only says that when you create a Circle it will be of type 'Shape' case class Circle(radius: Int) extends Shape case class Square(side: Int) extends Shape-- The | can be read as 'or' data Shape = Circle Int | Square Int -- Alternatively data Shape = Circle { radius :: Int } | Square { side :: Int }
ADT也可以嵌套:Shape是一种和类型,但其中每个选项本身可以是和类型或积类型。任何类型的领域模型都可以表示为和类型与积类型的组合。
Q:为什么和与积如此特殊?
除了作为建模的基本构件,它们还获得大多数FP语言的原生支持。积类型可以被解构和静态检查,而和类型可以用于模式匹配:
sealed trait Shape
case class Circle(radius: Int) extends Shape
case class Rectangle(width: Int, height: Int) extends Shape
// 'match' keyword allows us to pattern match on a
// specific option of the sum type
def area(shape: Shape): Double = shape match {
case Circle(r) => math.Pi * r * r
case Rectangle(w, h) => w * h // Note how rectangle's width and height
// are captured in 'w' and 'h'. It's possible
// because Rectange is a product type
}data Shape
= Circle { radius :: Double }
| Rectangle { width :: Double
, height :: Double }
-- In haskell different options of a sum type can
-- be handled with different 'functions'
area :: Shape -> Double
area (Circle r) = pi * r * r
area (Rectangle w h) = w * h -- width and height are captured in 'w' and 'h'
-- because Rectangle is a product type2、你需要的只有函数
认识一下你的新朋友——函数。你可能知道它的不同名字:getter、setter、构造函数、方法、builder、静态函数等。在OOP中,这些名字与不同的背景相关,并具有不同的属性。在FP中,函数始终只是一个函数——它接受值作为输入,并返回值作为输出。
使用函数不需要实例化任何东西(因为没有类),你只需要导入定义函数的模块并直接调用它。一个函数式程序只是ADT和函数的集合,就像前面的Shape例子一样。
一个函数应该有3个主要属性:
- Pure:纯粹性,没有副作用。函数不允许做超过其类型定义所规定的事情。例如,接受
Int值并返回Int值的函数不能修改全局变量、访问文件系统、执行网络请求等。它只能对输入值做一些运算并返回某些值。 - Total:完全性,为所有输入都返回值。对于某些属性会崩溃或抛出异常的函数是非完全函数或部分函数。例如,
div函数:类型声明承诺它会接收一个Int并返回一个Int。但是如果第二个参数是0,将会抛出“被零除”异常,因此它不是完全的。 - Deterministic:确定性,对于相同的输入会返回相同的结果。对于确定性函数,无论如何以及何时调用它,它总是返回相同的值。依赖于当前日期、时间、时区或一些外部状态的函数不是确定性的。
大多数编程语言都不能静态地保证这些属性,所以满足这些属性是程序员的责任。举例来说,Scala编译器很乐意接受不纯粹的、部分的和非确定性的函数:
// Just an example, don't do this at home
def isPositive(number: Int): Boolean = {
if (number == 0)
throw new Exception("meh") // Partial (non total)
else {
println("Calling isPositive!") // Impure (writing to std out is a side effect)
if (System.currentTimeMillis() % 2 == 0) // Non deterministic
number > 0
else
number < 0
}
}另一方面,在Haskell中,你不能(很容易地)写出一个不纯粹或非确定性的函数:任何类型的副作用函数都会返回一个IO,这个值表示“有副作用的”计算。完全性仍然由程序员掌控,因为你可以抛出异常或返回所谓的bottom,这将会终止程序。
isPositive :: Int -> Bool
isPositive number = undefined -- compiles but throws exception when called
-- Or
isPositive number = error "meh" -- sameQ:为什么我要关心一个函数是否满足这些性质?
如果一个函数满足这些性质,它就具有了“引用透明性”(详见另一篇文章)。简而言之,你就可以通过查看函数类型定义,准确地知道它能做什么和不能做什么。你可以无所畏惧的重构代码,因为引用透明性保证你不会出现任何问题。引用透明性让我们可以控制软件的复杂性。OOP中的重构可能是一场噩梦,因为直到真正运行程序并在头脑中构建一个模型后时,你才知道哪些对象在什么时候调用了什么方法。即便如此,这也不是一件容易的事。
3、你不能修改变量
Q:这是最奇怪的部分,我如何在不修改变量的情况下做出有用的东西?
如果你有一个变量person与 Person("Bob", 42) 绑定,你就不能将它重新绑定到Person("Bob",43)。你可以做的就是通过创建一个副本并指定你要改变的内容来创建一个不同的变量(就像我们之前讨论的那样)。变量是不可改变的,只用作别名或标记值,而不是一个物理引用或指向真实数据的指针。
Q:为什么不干脆在原地修改变量?
因为它破坏了引用透明性,正如我之前所说,引用透明性是FP的关键。它可以使你的生活更加轻松,而没有可变变量就是一个公平的代价。此外,没有可变变量意味着你可以免费获得线程安全的代码,不会再因为“只在周二晚上发生”的并发错误而浪费周末的时间。
不可变性是一个简单的概念,但是在多年的OOP开发经验之后,它就很难被接受了。我们经常看到人们在Scala中使用var,就是为了“让这个对象能工作”。一开始这样做是可以的,但一定要寻找一个不可变的实现。此外,在Haskell中没有这样的“技巧”,所以你必须从一开始就做到不可变。
4、你不能执行“for”循环
Q:我们的面包与黄油——“for”循环——你说FP中也没有?那如何对数组进行迭代?
没有突变就意味着没有for循环,因为它通常需要在满足条件之前修改一些计数器“i”。然而,我们有其它方法(递归和高阶函数)来实现同样的目的。
递归
你必须适应递归,因为它在FP中无处不在。例如,一个列表中所有数字之和看起来可能是这样的:
// 'List' is defined as a sum type so we can use pattern matching.
// There are two type constructors we need to check: one for empty list and
// one for head and tail:
def sum(lst: List[Int]): Int = lst match {
case Nil => 0 // Nil is a type constructor for an empty list
case x :: xs => x + sum(xs) // x :: xs looks weird but it's actually just
// a product type named '::' and can be rewritten as
// case ::(x, xs) => ...
// Scala allows infix operators for type constructors
// so it's possible to say 'case x :: xs'
}
sum(List(1,2,3,4,5)) // 15
// This is just an example, as there is a built in sum function that
// can be used as List(1,2,3,4,5).sum-- Similar to Scala version, List is just a sum type with two options
-- [] is a type constructor for an empty list
mySum :: [Int] -> Int
mySum [] = 0
mySum (x : xs) = x + (mySum xs)
-- We will step through the list building a sum expression until we hit
-- the empty list case which returns 0. That will close the loop and
-- the built up expression will be summed up使用递归数据结构是很常见的,比如列表或树。甚至自然数也可以用这种方式表示。遍历这些数据结构的自然方法是对类型构造器进行模式匹配,并将递归函数应用到数据结构的递归部分。一般模式是首先定义一个基本分支,比如空列表分支来终止递归,然后再定义一个一般的分支。
高阶函数
高阶函数将其它函数作为参数。说到迭代,你必须知道如何使用map和fold:
// Pass a function to transform every item in the list
List(1,2,3,4,5).map(n => n + 1) // List(2,3,4,5,6)
// Or shorter syntax
List(1,2,3,4,5).map(_ * 2) // List(2,4,6,8,10)
// Fold example. Sum all the values in a list
List(1,2,3,4,5).fold(0)((l, r) => l + r) // 15
// Multiply each number by 2, convert to string and
// produce a total string appending the results together
List(1,2,3,4,5).foldLeft("")((acc, number) => acc ++ (number * 2).toString) // "246810"-- Add 1 to every item in the list
map (+1) [1,2,3,4,5] -- [2,3,4,5,6]
-- Sum all the values
foldl' (+) 0 [1,2,3,4,5] -- 15
-- Multiply each number by 2, convert to string and
-- produce a total string appending the results together
foldl' (\acc n -> acc ++ show (n * 2)) "" [1,2,3,4,5] -- "246810"
-- foldl' (\acc n -> acc ++ show (n * 2)) "" [1,2,3,4,5]
-- ^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^ ^^^^^^^^^^^
-- name binary function that 'does the work' initial value list to foldQ:这些名字是什么意思?
map?不是像foreach那样吗?
是的,但只针对列表。很快你就会发现map不是用来转换列表的,而是根据我们想要映射的东西有不同的语义。如果你想了解更多——可以查看一下Functor,这是一个提供映射接口的高级类型。但是不要太担心Functor——只需要把map看着是一个知道如何迭代数据结构(如列表、树、字典等)的函数就可以了。
fold也有更深的含义,与Foldable有关。直觉告诉我们,它会接收一些数据结构并产生单个值,如求和。请注意,map与fold不同,它将函数独立地应用于每个值,而fold可以携带某种依赖于先前值的累加器。
还有更多的函数,但了解这两个函数足以让你在大多数迭代问题上走得更远。
5、你的代码不再是指令列表
在命令式语言中,你可以这样做:
object MyProgram extends App {
doThis()
doThat()
doSomethingElse()
printResult()
}这些函数有“副作用”,如它们会做一些事情。它们操作的结果是整个程序的状态发生了变化——一些文件被写入磁盘,在控制台输出,更新内部实体映射,等。一旦你调用这样的函数——它就确实被完全执行了。
好吧,这没什么新鲜的,这就是我通常的编程方式。
当然,但是在函数式程序中,直到最后一刻之前都不会执行任何操作。你的函数必须接收值并返回值,不允许有副作用。一个函数的输出是另一个函数的输入,而另一个函数又反过来为其它函数创建了输入,以此类推。
这段程序在FP中可能是下面这样的:
object MyProgram extends App {
unsafeRun( // <-- This guy takes your pure program
// and actually runs it
printResult( // --
doSomethingElse( // |
doThat( // |
doThis() // | This is your 'pure' part, nothing happened yet
) // |
) // |
) // --
)
}注意这里的unsafeRun函数(我们假定它是语言提供的)。在unsafeRun之前,我们所做的只是将函数粘在一起,并没有执行任何操作。我们正在构建某种执行计划——“这个函数首先被调用,然后根据它的输出,我们将调用这两个函数中的一个”,等等。
这也不是一个容易掌握的概念,因为我们习惯于在这里抛出一些额外的行为,来做一些事情,比如日志语句或设置一些标志,清除一个队列等等。你不能再这样做了,因为这些附加函数必须遵循类型约束并与其它函数组合。这是一件好事——它迫使我们对程序所做的事更有原则,并确保所有的东西都编码在函数的类型签名中。
6、关于null和异常
空值在命令式代码库中随处可见。null的问题在于,它是一个较低层次的抽象,被泄露到了更高级别的类型系统中。如果我看到一个函数会返回一个Person,(假定函数是完全的)那么我期望得到一个有名字、地址等任何信息的Person。 null不是一个Person。null通常用于表示不存在或者是某种阻止函数返回正确值的内部故障。如果函数在某些情况下无法返回一个Person,则应该在其类型声明中进行说明。在FP中,我们可以用和类型表示不存在。
// A simple sum type that has two options
sealed trait Option[A]
// A value of some type 'A' (product type with a single field)
case class Some[A](value: A) extends Option[A]
// Type constructor that represents absence of a value
case class None[A]() extends Option[A]
// Instead of throwing an exception or crashing the function will
// return a *value*.
def divide(dividend: Int, divisor: Int): Option[Int] =
if (divisor == 0)
None()
else
Some(dividend / divisor)
// And compare it to the usual non total and unsafe function.
// By looking at the type signature we have no idea if the
// function is total or not, will it throw or not
def divide(dividend: Int, divisor: Int): Int =
if (divisor == 0)
throw new Exception("meh")
else
dividend / divisor
// The 'Option' sum type is available in the Scala standard library-- Simple sum type with two options
data Maybe a = Just a | Nothing
-- Safe total function that never throws
divide :: Int -> Int -> Maybe Int
divide dividend divisor = if divisor == 0 then Nothing else Just (dividend / divisor)
-- Maybe is available in Data.Maybe module如果一个函数返回一个Person的Maybe或Option封装,它明确表示——不保证返回Person。调用者必须检查返回值是Some还是None,这也意味着不再有null解引用问题或null指针异常。
如果你仔细想想,会发现null是一种低层原语,它与运行时系统有关,而与你的程序逻辑无关。当你使用带有垃圾收集功能的高级语言写代码时,你并不关心何时以及如何在内存中分配对象,也不关心你的函数生成的机器码是什么。这就是高级语言的作用——它们创建了一个抽象概念,所以你不必考虑细节。null打破了这种抽象,所以代码会被奇怪的q! = null检查甚至更糟糕的解引用问题所污染。
同样地,异常也是如此。没有必要为了处理异常情况而引入使用特殊语法的特殊机制。在纯程序中,可以用普通值标识不存在、失败或异常。用throw e抛出异常会让函数变得部分化(非完全),这又打破了引用透明性并制造了问题。
如果你使用JVM和java库,你就不得不处理异常问题。在一些特殊情况下使用异常是可以的,比如IO,但要确保它是函数类型的一部分——调用者必须知道函数会抛出、可以抛出什么样的异常,这些约定都可以在编译时检查。
7、Functors, Monads, Applicatives?
Q:我经常听到FP人员讨论这些事情,但对我来说没有任何意义。有什么简单的解释吗?
人们发现了一些通用模式,并根据范畴理论给它们命名。Functors、Monads和Traversables是相当强大和常见的抽象,你到处都能看到它们。这个主题足够单独写一篇文章。但是现在,你还不需要担心它。你最终会了解它们的(甚至可能自己重新发明它们)。熟悉函数组合、高阶函数和多态函数,然后再阅读类型类。在那之后,Functors和Monads应该会自然出现。这里的要点是,没有魔法,除了我们在本文中已经讨论过的纯函数和函数组合之外,也没有更多的东西。
希望这篇文章有帮助,如果没有——请给我反馈。正如有人所说,“一旦你理解了Monads,你就失去了向别人解释的能力”,所以我希望这篇文章不会离OOP开发者的日常经历太远。谢谢你的阅读,请享受你的FP之旅。



